Acceleration, Gravity, and more
One Dimensional Motion
|
The LabThe motion of objects has been well characterized for hundreds of years. Using some fairly simple equations, we can make predictions about the relationship between velocity, acceleration, distance, and time. While these equations can be modified to apply to motion in three dimensions, it requires breaking motion down into component vectors. Therefore, it is often easiest to begin by looking at motion along just one of these dimensions (ie. an object that only moves in a straight line). One system where this is especially applicable is that of falling objects.
In this experiment, you will try to develop a strategy for determining the constant "g" with the equations of motion. You will then compare your experimentally determined value to the known true value to establish the validity of your experiment. |
Process
To begin, my group and I, created an experiment that could be easily recorded and replicated multiple times with the time and tool available to us. After much debating we measure the acceleration of a falling pen by filming its decent in slow motion with an active timer and ruler in frame. We did this because when conducting it, we had to keep in mind the velocity equation: distance/time and making sure we had a way to record these. Using these recordings we could plug in our values to provided equations. Using the video we were able to obtain our results by recording the time displayed on the timer at specific points in the pens decent. Once we recorded our data, we began attempting to calculate the acceleration with the provided formulae and contraints:
g(true) = Gravity = 9.80665 m/s2
Δv = a⋅Δt (1)
Δx = vo⋅Δt + 12⋅a⋅(Δt)^2 (2)
Δx = v+vo^2⋅Δt (3)
v^2 = vo^2 + 2⋅a⋅Δx (4)
% error =(your value) - (true value)(true value)100 (5)
*Δv is final minus initial velocity
*Δt is usually just t, assuming initial time is 0
*Δx is final minus initial position, and is often just x if initial position is 0
Δv = a⋅Δt (1)
Δx = vo⋅Δt + 12⋅a⋅(Δt)^2 (2)
Δx = v+vo^2⋅Δt (3)
v^2 = vo^2 + 2⋅a⋅Δx (4)
% error =(your value) - (true value)(true value)100 (5)
*Δv is final minus initial velocity
*Δt is usually just t, assuming initial time is 0
*Δx is final minus initial position, and is often just x if initial position is 0
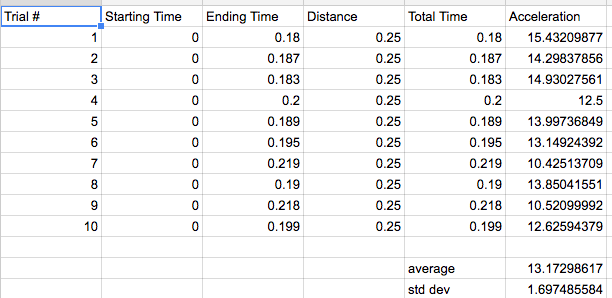
After choosing the second equation as our pathway to finding the acceleration, we created a spreadsheet with the assistance of Mr. Ruppel in order to calculate our accelerations without the incredible mental labor. Here is what we found:
To find the acceleration, we used the values we recorded and plugged them into the equation, solving for "a." After doing this we repeated the experiment ten times and proceeded to find the average acceleration, the standard deviation, and the % of error, which was about 57.14%. We can assess and explain these numbers by the standard random errors in the process and recording of the experiment, such as: added force applied to the pen, the pen interfering with anything while descending, inaccuracy of our timers, approximation of values, inaccuracy of our distances, angles of video, and more. The video is imbedded below for download and viewing pleasures of those interested in the experiment.
| Experiment Footage | |
| File Size: | 875 kb |
| File Type: | mov |