Lets redesign the coke can
Pow #6: Canalysis
Problem Statement:
Why does Coca-Cola have the can it does? Is there a better alternative? Well in this problem we set out to find out. By keeping the volume of the can a constant we messed around with the height and radius of the can we tried to figure out if there was a can that was cheaper to make that would give the company even more profit.
Process/Solutions:
To do this we found the height, diameter and radius of a normal Coke can in order to solve for the volume. I did this by using the volume formula of: V=πr^2h (h=height, r=radius). Using the information we found we solved for the volume, which will be the constant for all the cans. The volume ended up being about 365 m^3. After I did this I created two alternative cans by manipulating the height of the can and solving the volume formula in terms of radius. After I did this I imputed the information into the Surface Area equation (SA=[2πr^2] + [2πrh]). Then I took the surface area and multiplied it by 0.00016 to get the price that it would cost to manufacture the can. The information for all three is below:
Original Can Can #2 Can #3
Height 12.1 cm 2 cm 100 cm
Radius 3.1 cm 7.621 cm 1.0778 cm
Diameter 6.2 cm 15.243 cm 2.1557 cm
Volume 365 cm^3 365 cm^3 365 cm^3
S.A. About 296 cm^2 About 461 cm^2 About 685 cm^2
Cost $0.04736 $0.07376 $0.1096
After finishing this process we had to choose which can is the best option, this is of course the original can because it holds the same amount and ultimately cost less to manufacture.
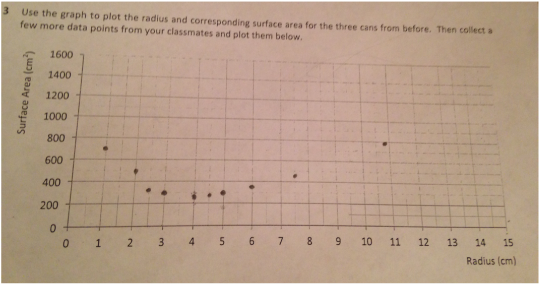
The next step in the problem was to graph the information of the class. With the x-axis being the radius of the can and the y-axis being the surface area of the can we found the lowest approximate point and used that as the lowest cost of any can with a volume of 365 cm^3. The graph looked like this:
With this information we decided that the lowest point had a radius of 3.8 cm. After this we formally rewrote the volume equation in terms of height: V=πr^2 /πr^2 = h=v/πr^2. We then rewrote the surface area in terms or radius like so: SA=(2πr^2)+(2πr(v/πr^2)) = 2πr^2+2v/r. Using these new formulas we inputted the lowest radius to find the surface area of the lowest can on the graph, the SA ended up being 282.8cm^2. The can ended up looking slightly shorter and a little fatter than the original can. After finding all this out we figured out the cost of manufacturing this can using the same process as before and multiplied that by the amount of coke sold in a year (19 billion). After we did this we compared the cost to that of the original can and found that if Coca-Cola would implement the new design it would save $38 million. After a brief discussion with the class, we decided that the amount of money they would save was too small of savings compared with the money they annually make, so it would be easier if Coke did not implement the new design and kept using the original.
Reflection:
I feel that this problem really gave another aspect to volume and how it can be inputted into everyday life. It also introduced and incorporated surface area in an interesting and well done way. Personally I think that the Habit of a Mathematician that I used most during this process was Following a Pattern. The way that I used this was by following a set process of working back the volume to find the radius, finding the surface area and so on. Over all the problem provided a fun way to learn volume, surface area and how to manipulate the formulas to find whatever you need.
Reflection:
I feel that this problem really gave another aspect to volume and how it can be inputted into everyday life. It also introduced and incorporated surface area in an interesting and well done way. Personally I think that the Habit of a Mathematician that I used most during this process was Following a Pattern. The way that I used this was by following a set process of working back the volume to find the radius, finding the surface area and so on. Over all the problem provided a fun way to learn volume, surface area and how to manipulate the formulas to find whatever you need.